SDPsite: prediction of protein active and specific recognition sites from sequence and structure |
 |
Home & Submit job |
Algorithm & |
Contact us |
Gallery of examples |

SDPsite is a tool for identification of protein active and other functional sites, based on spatial clustering of SDPs (specificity-determining positions, described here) with CPs (conserved positions).
The algorithm contains three parts:
- Prediction of SDPs
- Prediction of CPs
- Mapping predictied positions onto structure and construction of the best cluster
Each of these parts can be run separately.
Prediction of SDPs
SDPs for pre-defined specificity groups
The algorithm for prediction of SDPs is described in Kalinina et al. (2004) Prot Sci 13: 443-456. The input data of the algorithm are a multiple protein alignment divided into specificity groups. Proteins of the same specificity group have same specificity to the ligand (or DNA, or another interacting protein), and proteins of different specificity groups may have different specificity. Let's consider each position of the alignment independently. To evaluate if the considered position is SDP, calculate its mutual information, a measure of how well the distribution of amino acids in the positions is associated with grouping bu specificity:
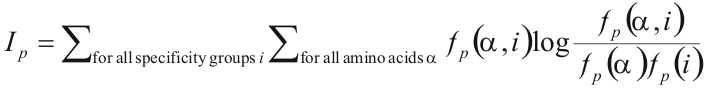
where
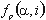 is the ratio of the number of occurrences of residue
is the ratio of the number of occurrences of residue 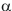 in group i at position p to the length of the whole alignment column;
in group i at position p to the length of the whole alignment column; 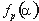 is the frequency of residue
is the frequency of residue 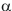 in the whole alignment column;
in the whole alignment column; 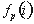 is the fraction of proteins belonging to group i.
is the fraction of proteins belonging to group i.
We introduce a number of corrections to account for properties of real biological data (discussed in Kalinina et al. (2004) Prot Sci 13: 443-456). Then, using random shuffling of the column, we calculate the mean 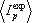 and the variance
and the variance 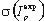 of expected column mutual information, and then a z-score of the position:
of expected column mutual information, and then a z-score of the position:
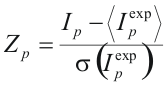
A high value of Z-scores indicates a position, where the amino acid distribution is much closer associated with grouping by specificity than for an average position of the alignment, and thus, which is likely to be an SDP. Given a series of Z-scores corresponding to every position of the multiple alignment, one needs to evaluate the significance of the Z-scores in order to tell whether the observed Z-score is sufficiently high to indicate a SDP. SDPpred uses an automated procedure for setting the thresholds based on the computation of the Bernoulli estimator. The observed Z-scores are oredered by decrease: 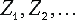 . The threshold is defined as:
. The threshold is defined as:
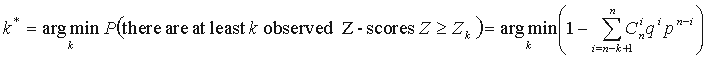
where 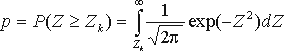 ,
, 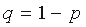 .
.
Thus, we conclude that k* highest-scoring position are non-randomly distributed and designate them SDPs. Probability

is called statistical significance of the set of k* positions.
Automated indetification of specificity groups
SDPsite does not request user-defined specificity groups. Instead, an automated procedure for identification of specificity groups is implemented. The user is requested to provide an unrooted tree, than SDPsite performs analysis similar to Evolutionary Trace.
The root of the tree is assumed to be placed in the middle of the longest path between leaves. Than a series of groupings obtained from dissection of the tree at different distance from the root is considered (see fig. below).
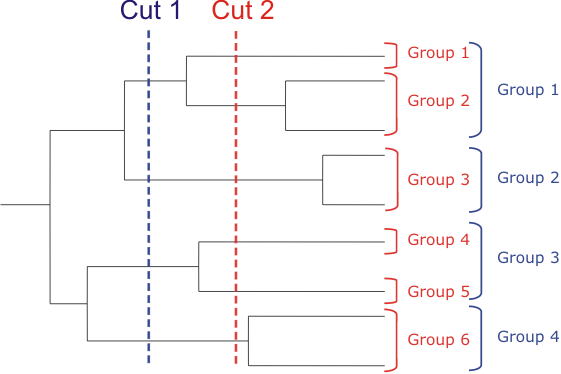
Groups containing less than three sequences were not considered. Than for each grouping we find SDPs as described above and calculate the statistical significance P* for the obtained set of SDPs. The calculated Z-scores are corrected:
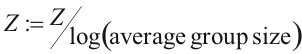
This correction is needed, because z-score logarithmically increases with the increase of the group size. Grouping that generates set of SDPs with the least P* is called best, or correct, grouping.
Prediction of CPs
There are different ways to measure conservation score of a position. SDPsite implements one proposed be Sander and Schneider (Sander and Schneider (1991) Proteins 9: 56-68):
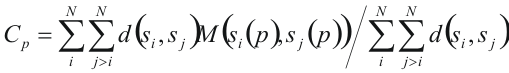
where
N is the number of sequences in the alignment
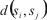 is distance between sequences si and sj, equal to
is distance between sequences si and sj, equal to 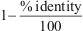
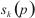 is amino acid in sequence k in position p
is amino acid in sequence k in position p
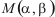 is amino acid substitution matrix (BLOSUM62)
is amino acid substitution matrix (BLOSUM62)
For each Cp, its statistical significance is calculated. First, we calculate the background distribution, which is distribution of conservation scores of columns made up of one random position from each sequence. For each Cp, 104 random comservation scores Cprand are calculated, and then z-score is computed as:
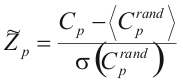
As alignment of two random sequences has a non-zero weight, the obtained z-scores has to be centered:
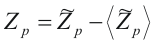
Then we select the correct number of CPs using the Bernoulli estimator procedure described above.
Construction of the best cluster
To construct the best cluster, SDPsite requires a 3D structure of one of the proteins of the considered alignment. On the 3D structure, it locates predicted SDPs and CPs and cluster them using layered of tightness set function algorithm (Mirkin and Muchnik (2002) Appl Math Lett 15(2): 147-151). The layered clusters are constructed as follows. The graph vertices correspond to the set of SDPs and CPs on the 3D structure. Initial cluster H0 includes all graoh vertices. Then, for each vertex i, ins weight is calculated:
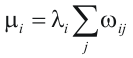
where j indexes all the other vertices from H0 and 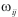 is calculated as follows:
is calculated as follows:
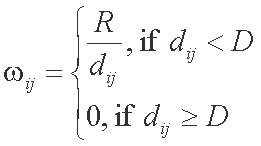
where
dij is the Euclid distance between closest atoms of amino acids i and j
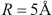 is average distance between centers of contacting atoms
is average distance between centers of contacting atoms
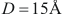 is a technical parameter reflecting influence distance of atom
is a technical parameter reflecting influence distance of atom
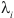 =1, if vertex i is a CP, and 1 otherwise. So weight of CPs is generally lower than weight of SDPs, so that the algorithm will not choose a group of conserved hydrophobic residues as the best cluster.
=1, if vertex i is a CP, and 1 otherwise. So weight of CPs is generally lower than weight of SDPs, so that the algorithm will not choose a group of conserved hydrophobic residues as the best cluster.
Then, find set of vertices 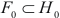 , for which
, for which 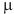 achieves its minimum and equals
achieves its minimum and equals 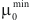 . Construct cluster
. Construct cluster 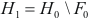 . This procedure is repeated until the empty set is achieved. Thus a series of clusters is constructed:
. This procedure is repeated until the empty set is achieved. Thus a series of clusters is constructed: 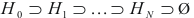 . The cluster, for which
. The cluster, for which 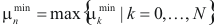 , is chosen as the most significant, or best, cluster.
, is chosen as the most significant, or best, cluster.
Format requirements
The alignment is submitted in the standard GDE format, e.g.:
The tree is submitted in the Newick format: